Sunday, November 16, 2014
Single GPU-Powered Node 4x Faster Than 50-node Spark Cluster
And BIDMat is just one component of their full BIDMach software stack illustrated below (illustration also from their dissertation).
Intel MKL and GPU/Cuda are of course off-the-shelf libraries. Butterfly mixing is a new 2013 technique by the same two authors that updates a machine learning model "incrementally" by using small subsets of training data and propagating model changes to neighboring subsets. They do not state it explicitly, but these network communication diagrams between the small subsets resemble the butterfly steps in the Fast Fourier Transform algorithm.
Kylix is an even newer (2014) algorithm, again by the same two authors, that further optimizes the butterfly approach by varying the degree of each butterfly node (the number of butterfly nodes each butterfly node must communicate with) in a way that is optimized for real-life power-law data distributions.
Finally, part of their overall approach is what they have coined "rooflining", which is where they compute the theoretical maximum communication and computation bandwidth, say of a GPU, and ensuring that their measured performance comes close to it. In their dissertation, they show they reach 80-90% of CPU/GPU theoretical maximums.
By doing so, the authors have turned GPU hype into reality, and have implemented numerous machine learning algorithms using their BIDMach framework. Now it remains to either make BIDMach available for commercial production use, or to incorporate the concepts into an existing cluster framework like Spark.
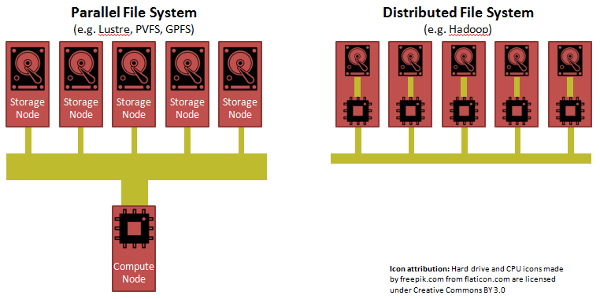
Parallel vs. Distributed file systems: Time for RAID on Hadoop?
The long-standing wisdom is that RAID is not beneficial for Hadoop data nodes. This wisdom is traced back to the venerable Hadoop: The Definitive Guide, which cites a 2009 Apache forum posting from Yahoo! engineer Runping Qi reporting experimental results showing JBOD to be faster than RAID-0.
The reasons cited in the Hadoop book are:
- HDFS has redundancy anyway, and
- RAID-0 slows down the entire array to match the speed of the slowest drive in the array
We can look toward "parallel" file systems from the world of High Performance Computing (HPC) for inspiration. The paradigm in HPC is to separate compute from storage, but to have a really fast network, but more importantly to have a "parallel file system". A parallel file system aggregates the bandwidth from many storage nodes to feed a compute node.
While Hadoop was able to achieve its performance through its clever insight of shipping code to data, each CPU in a Hadoop cluster has to suck its data from a single disk through a straw.
The limiting factor for both HPC and Hadoop is the slow transfer rate (1 Gbps) out of a hard drive. HPC addresses this bottleneck by:
- striping data across nodes,
- storing data across nodes in a round-robin fashion, rather than the more random approach that Hadoop takes
- using high-bandwidth links in the cluster (e.g. 40 Gbps Infiniband vs. 1 Gbps or 10 Gbps Ethernet
- using network DMA (Infiniband) instead of a heavy software stack (Ethernet)
There have been a couple chinks in the armor of the "No RAID for HDFS" received wisdom in the past couple of years. The book Pro Apache Hadoop, Second Edition, just published this month, provides one specific exception to the rule:
Some Hadoop systems can drop the replication factor to 2. One example is Hadoop running on the EMC Isilon hardware. The underlying rationale is that the hardware uses RAID 5, which provides a built-in redundancy, enabling a drop in replication factor. Dropping the replication factor has obvious benefits because it enables faster I/O performance (writing 1 replica less).Another is Hortonworks in 2012, which gives credence to the idea of using RAID-0, but at most only pairs of disks at a time.
It seems that we could have the best of both worlds if each node in a Hadoop cluster had parallel I/O across many disks, such as can be provided by RAID-0. As for the concern that RAID-0 is slowed to the speed of the slowest drive, well, the same is true of PVFS.
So should RAID-0 be used in Hadoop data nodes to speed up I/O to the CPU? Probably not, and here's why. CPUs for the past decade have plateaued on clock speed and have instead been adding cores. And there is a recommendation that there be a 1:1 ratio between "spindles to cores". For the purposes of I/O, multiple hard drives joined in RAID-0 would be considered a single spindle. So one could imagine a single 12-core CPU connected to 12 RAID-0 pairs, for a total of 24 drives. But as core count goes up over the upcoming years, and if dual- and quad-CPU motherboards are considered instead, this scenario becomes the exception.
Sunday, November 9, 2014
Data Locality: HPC vs. Hadoop vs. Spark
The big advance Hadoop brought over classic High Performance Computing (HPC) is data locality. Hadoop brings the compute to the data. (HPC compensates by having faster interconnects such as Infiniband and high-bandwidth storage.)
The big advance Spark brought over Hadoop is storing data in each node's RAM instead of each node's disk. Spark's leveraging of data locality is very similar to that of Hadoop's: namely, computation is assigned to occur where the data resides.
Except Spark 1.2 is set to improve that a bit. In a just published paper, AMP Lab contributor Shivaram Venkataraman et al propose assigning the reduce task to the node that happens to have the largest map output, thus minimizing data movement.
This advance is currently slated for Spark 1.2, in Jira ticket SPARK-2774
There are other advances described in the Venkataraman et al paper, namely, when sampling subsets of data such as BlinkDB does, Spark could greedily take whatever data happens to be present on nodes with available compute, and call that the sample. There is no set Spark release for that feature, which the paper calls KMN.
Four Reasons for Immutable HDFS Archive
Two years ago, when I first joined Michael Walker's Data Science & Business Analytics Meetup, the form asked (and still asks) "What important truth do very few people agree with you on?" My answer was "Data should never be deleted". At the time, I had no idea what Data Science was and had barely been introduced to Big Data, but it was a dictum I lived by, much to the consternation of my bosses over the past two decades when it came time to approve purchases of hard drives.
Well, I may have to update my profile, because it seems more and more people are agreeing with me. As I blogged on the January, 2014 Boulder/Denver Big Data Meetup, the discussion format came to a consensus that all ingested data should be kept intact as-is as an immutable data store, and that processed data should be stored in some kind of data warehouse for the actual analytics. I wrote then that it was good to have that pattern, which was in the making for a couple of years, finally codified as a pattern.
It's even more solidified now. The two most common motivations given are:
1. Bugs
You might discover a bug in your processing code, and so you may need to reprocess all the original data with the corrected code.2. New Derived Metric
You might discover you need to track clicks per second rather than just clicks per minute. With the original data still around, it becomes possible to resummarize the raw data.Two Other Reasons
But here are two other reasons, not usually stated when this pattern is presented:3. New Data Enrichment
Suppose in your summarized data you don't store social security number even though it exists in the original data. Then your company just obtained the services of data provider, and you're now able to get household income based on social security number. Now you can append this data as another column in the analytics database.4. Reapply Machine Learning to Bigger Data Set
This is perhaps the most important reason of all, due to the The Unreasonable Effectiveness of Data. As more data becomes available over time from the original data streaming source, machine-learned models can be improved.Semantic Similarity Metrics
Data Science is more than just statistics and machine learning on numbers. A lot of data is "unstructured," which means text (or worse, both text and numbers). While natural language processing has been around for half a century, its importance in the fields of Big Data and Data Science is growing and can no longer be ignored if one is to maintain competitive advantage.
There is a planet full of tools, and herein I describe one grain of sand out of that planet: Semantic Similarity Metrics.
Given a document of text (e.g. a Facebook posting or an e-mail), we can turn it into a set of words or a bag of words. A bag of words is like a set of words, except it also includes the multiplicity. E.g. the miniature document "Now, come now" represented as a set of words would be {"now", "come"} whereas as a bag of words would be
| Word | Freq |
|---|---|
| now | 2 |
| come | 1 |
Sets of words and bags of words can alternatively be considered as Boolean vectors and numeric vectors, respectively.
A common need when processing documents is to evaluate their similarity, e.g. to determine if they are duplicates, or to determine how close a sample document might be to a "reference" document (e.g. for automated essay scoring). There are various similarity metrics available, for both Boolean and numeric vectors.
Similarity Metrics for Boolean Vectors
Recall that what we mean by "Boolean Vectors" are really just sets, and it is easier to think about and discuss these as sets rather than as literal Boolean vectors, so we use set notation.
Jaccard Index
The Jaccard Index is the simplest metric:
\[\frac{\left|A \cap B\right|}{\left|A \cup B\right|}\]
Dice-Sørensen
The Dice-Sørensen (aka just Dice or just Sørensen) is similar to the Jaccard.
\[\frac{2\left|A \cap B\right|}{\left|A\right| + \left|B\right|}\]
They both give scores in the range [0,1]. But Dice emphasizes similarity, especially in the cases where one set is larger than the other. However, Dice does not satisfy the triangle inequality and thus is not a true metric in the mathematical sense of the word.
Tversky
Tversky is a generalization of Jaccard and Dice, in that Jaccard and Dice become just special cases of Tversky:
\[\frac{2\left|A \cap B\right|}{\left|A \cap B\right| + \alpha\left|A-B\right| + \beta\left|B-A\right|}\]
We arrive at Jaccard with \(\alpha=\beta=1\) and at Dice with \(\alpha=\beta=0.5\). But by varying \(\alpha\) and \(\beta\) to be different from each other, we can apply Tversky to situations where we wish to treat documents asymmetrically. For example, if instead of documents A and B that are treated equally, we have a reference set R (perhaps some sort of answer key) and a user set U, then by setting \(\alpha\) high we can "punish" the user for missing words that were expected in R. Alternatively, we could set \(\beta\) high to "punish" the scoring for not finding the best R that best matches the user input U.
Similarity Metrics for Numeric Vectors
Instead of having seta A and B, we now consider numeric vectors X and Y, which are frequency counts in our bag of words.
Tanimoto
The Tanimoto metric is the numeric vector generalization of the Jaccard index for Boolean vectors:
\[\frac{X \cdot Y}{\left|X\right|^2 + \left|Y\right|^2 - X \cdot Y}\]
Here, the dot represents the vector dot product.
Cosine
The cosine similarity metric is similar in appearance to Tanimoto:
\[\frac{X \cdot Y}{\left|X\right| \left|Y\right|}\]
The cosine has the appealing property that 0 means a 90 degree separation, or complete orthogonality.